Walton's Blog
Go back

R：基础计量

Table of Contents

Open Table of Contents

Preface

The question isn’t whether you’ve omitted anything, it’s how important the omission is.

Your last line of defense is your gut. 如果你在直觉上感觉都有些不对劲，那大概率是错的。

A. Regression

💡 寻找与主效应相关的变量，将他们都控制住

1. Error Terms / Residual

Y=β0+β1X+ϵY = \beta_0 + \beta_1 X + \epsilon

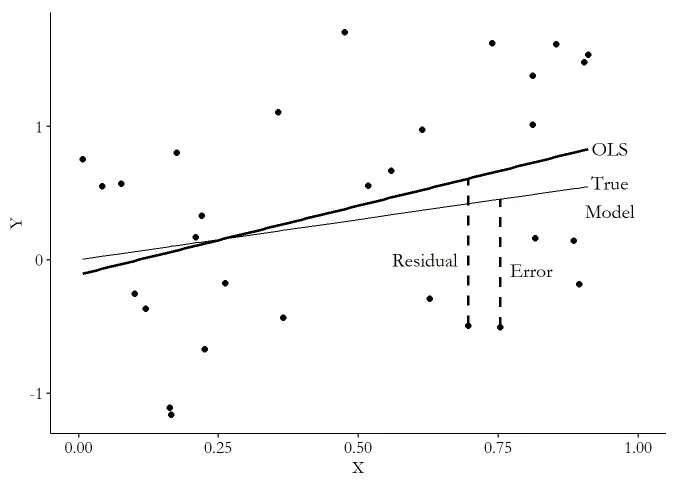
拟合模型中未知的部分就是Residual，未知的部分则是Error Error是由于模型的局限而导致的，Residual则还包括了样本的局限 由此，引出了外生性假设

2. Hypothesis Testing

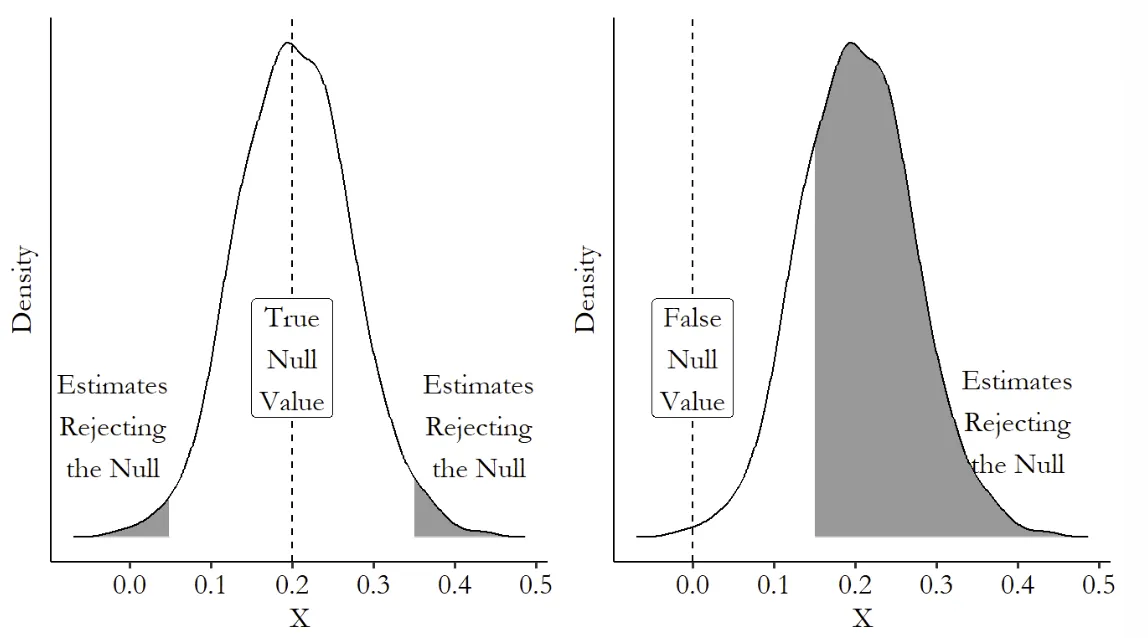
假设检验提供了一个捷径，我们通过拒绝 β=0\beta = 0 来告诉别人我的模型是对的 但是，不具有显著性的变量，不意味着他的估计就是错的，他只是在统计上不重要 不要通过修改数据来获得显著性 Never P-hacking 此外，显著性通过不意味着估计真实，如果标准误很大，那么研究结论很可能是一个侥幸 最后，显著性不是研究的全部，研究结论的重要与否更取决于你的故事

3. Variables

library(car)
linearHypothesis(fit, hypothesis.matrix)

4. Standard Errors

  1. 异方差下的标准误修正：Sandwich Estimator 和 Huber-White Standard Errors
library(tidyverse)

m1 <- causaldata::restaurant_inspections %>%
  lm(inspection_score ~ Year + Weekend, data = .) # 拟合

# 法1：使用AER包计算
library(AER); library(sandwich)
coeftest(m1, vcov = vcovHC(m1))
# 法2：也可以直接用modelsummary汇总出结果
library(modelsummary)
msummary(m1, vcov = 'robust',
		 stars = c('*' = .1, '**' = .05, '***' = .01))
# 法3：也可以用fixest直接进行回归分析
library(fixest)
feols(inspection_score ~ Year + Weekend, data = df, se = 'hetero')
  1. 时间自相关下：Heteroskedasticity- and Autocorrelation-Consistent (HAC) Standard Errors、Newey-West estimator
library(tidyverse)

m2 <- causaldata::restaurant_inspections %>%
  group_by(Year) %>%
  summarize(Avg_Score = mean(inspection_score),
			Pct_Weekend = mean(Weekend)) %>%
  dplyr::filter(Year <= 2009) %>%
  lm(Avg_Score ~ Pct_Weekend, data = .) # 拟合

library(AER); library(sandwich)
coeftest(m2, vcov = NeweyWest)
  1. Hierarchical Structure：clustered standard errors、Liang-Zeger standard errors
library(tidyverse)

m1 <- causaldata::restaurant_inspections %>%
  lm(inspection_score ~ Year + Weekend, data = .) # 拟合

# 法1
library(AER); library(sandwich)
coeftest(m1, vcov = vcovCL(m1, ~Weekend))
# 法2
library(modelsummary)
msummary(m1, vcov = ~Weekend,
		 stars = c('*' = .1, '**' = .05, '***' = .01))
# 法3
library(fixest)
feols(inspection_score ~ Year + Weekend,
	  cluster = ~ Weekend,
	  data = df)
  1. 最后，Bootstrap，解决样本偏误问题的最完美的标准误
library(tidyverse); library(modelsummary); library(sandwich)

m1 <- causaldata::restaurant_inspections %>%
  lm(inspection_score ~ Year + Weekend, data = .) # 拟合

msummary(m1, vcov = function(x) vcovBS(x, R = 2000),
		 stars = c('*' = .1, '**' = .05, '***' = .01))

5. Additional Regression Concerns

  1. 样本权重 Sample Weights 当样本有偏时，可以通过调整权重来控制样本的分布
library(tidyverse); library(modelsummary)

df <- causaldata::restaurant_inspections %>%
  group_by(business_name) %>%
  summarize(Num_Inspections = n(),
			Avg_Score = mean(inspection_score),
			First_Year = min(Year))

# Add the weights argument to lm
m1 <- lm(Avg_Score ~ First_Year,
		 data = df,
		 weights = Num_Inspections)

msummary(m1, stars = c('*' = .1, '**' = .05, '***' = .01))

# 如果权重很复杂，可以 library(survey)
  1. 共线性 Collinearity 一般情况下不会有完美的共线问题，但是当两个变量间 VIF 高于 0.9 时还是需要处理一下 VIF 高于 0.9 指的是 A=β0+β1BA = \beta_0 + \beta_1 B，回归发现 R2R^2 大于 0.9
library(tidyverse)

m1 <- causaldata::restaurant_inspections %>%
  lm(inspection_score ~ Year, data = .) # 拟合

library(car)
vif(m1)
  1. 测量误差 Measurement Error 经典测量误差可以不用处理 而当测量误差与自变量相关时，则需要进行处理
  2. 惩罚回归 Penalized Regression
library(tidyverse); library(modelsummary); library(glmnet)

# 数据处理
df <- causaldata::restaurant_inspections %>%
  select(-business_name)
X <- model.matrix(lm(inspection_score ~ (.)^2 - 1,
					 data = df))
numeric.var.names <- names(df)[2:3]
X <- cbind(X,as.matrix(df[,numeric.var.names]^2))
colnames(X)[8:9] <- paste(numeric.var.names,'squared')
Y <- as.matrix(df$inspection_score)
X <- scale(X); Y <- scale(Y)

# 找到一个最好的lambda，也就是cv.lasso$lambda.min
cv.lasso <- cv.glmnet(X, Y,
					  family = "gaussian",
					  nfolds = 20, alpha = 1)

# 运行真正的lasson模型
lasso.model <- glmnet(X, Y,
					  family = "gaussian",
					  alpha = 1,
					  lambda = cv.lasso$lambda.min)

# 查询那个变量被抛弃了，表现为-
lasso.model$beta

B. Matching

💡 找到一个除了主效应外，没有其他变化的样本

1. Weighted

匹配体现在数据表中，通过加权的方式来影响数据的生成与回归的结果

2. Mahalanobis Distance Matching

基于 Mahalanobis Distance 的传统距离匹配

library(Matching); library(tidyverse)
br <- causaldata::black_politicians

# 被解释变量
Y <- br %>% pull(responded)
# 解释变量
D <- br %>% pull(leg_black)
# 用于匹配的变量
X <- br %>%
  select(medianhhincom, blackpercent, leg_democrat) %>%
  as.matrix()

# Weight = 2 指定使用 Mahalanobis distance
M <- Match(Y, D, X, Weight = 2, caliper = 1)
summary(M)

# 将匹配结果取出
matched_treated <- tibble(id = M$index.treated, weight = M$weights)
matched_control <- tibble(id = M$index.control, weight = M$weights)
matched_sets <- bind_rows(matched_treated, matched_control) %>%
  group_by(id) %>%
  summarize(weight = sum(weight))
# 与原始数据合并
matched_br <- br %>%
  mutate(id = row_number()) %>%
  left_join(matched_sets, by = 'id')

# 通过加权的方式加入到回归中
lm(responded ~ leg_black, data = matched_br, weights = weight)

3. Coarsened Exact Matching

Mahalanobis Distance 忽略了一些变量的作用，他会删除一些变量 如果我们假设所有的变量都很重要，就需要进行精确匹配 然而精确匹配要求距离为0，对于连续变量而言几乎不肯能有距离为0的变量 因此有必要先对变量进行粗化，将其作为类似类别的变量再进行匹配

library(cem); library(tidyverse)
br <- causaldata::black_politicians

# 取出需要用于匹配的变量，包括解释变量和被解释变量
brcem <- br %>%
  select(responded, leg_black, medianhhincom,
         blackpercent, leg_democrat) %>%
  na.omit() %>%
  as.data.frame() # Must be a data.frame, not a tibble

# 粗化变量
# 对于连续变量可以自动处理，但是二元变量需要手动处理

# 通过分位数来切割
# 这里数字为6，其实是分为了5类，去了中间的4个节点
inc_bins <- quantile(brcem$medianhhincom, (0:6)/6)

# 通过均匀分配来切割
create_even_breaks <- function(x, n) {
  minx <- min(x); maxx <- max(x)
  return(minx + ((0:n)/n)*(maxx-minx))}
# 与之前相同，6表示分为5类
bp_bins <- create_even_breaks(brcem$blackpercent, 6)
# 对于2维变量分为两类就行
ld_bins <- create_even_breaks(brcem$leg_democrat, 2)

# 记录区间
allbreaks <- list('medianhhincom' = inc_bins,
                  'blackpercent' = bp_bins,
                  'leg_democrat' = ld_bins)

# 匹配
c <- cem(treatment = 'leg_black', data = brcem,
         baseline.group =  '1',  # baseline.group 必须是对照组 treated group
         drop = 'responded',     # 被解释变量不应用于匹配
         cutpoints = allbreaks,
         keep.all = TRUE)

# 将匹配结果（权重）取出
brcem <- brcem %>%
  mutate(cem_weight = c$w)

# 回归
lm(responded~leg_black, data = brcem, weights = cem_weight) %>% summary()
# 也能用att
att(c, responded ~ leg_black, data = brcem)
# 论文中的回归结果
m1 <- lm(responded ~ leg_black*treat_out + nonblacknonwhite +
           black_medianhh + white_medianhh + statessquireindex +
           totalpop + urbanpercent, data = br, weights = cem_weight)
msummary(m1, stars = c('*' = .1, '**' = .05, '***' = .01))

4. Entropy Balancing

library(ebal); library(tidyverse); library(modelsummary)
br <- causaldata::black_politicians

# 被解释变量
Y <- br %>% pull(responded)
# 解释变量
D <- br %>% pull(leg_black)
# 匹配变量
X <- br %>%
  select(medianhhincom, blackpercent, leg_democrat) %>%
  # Add square terms to match variances if we like
  mutate(incsq = medianhhincom^2,
         bpsq = blackpercent^2) %>%
  as.matrix()

# 匹配
eb <- ebalance(D, X)

# 取出匹配结果
# Noting that this contains only control weights
br_treat <- br %>%
  filter(leg_black == 1) %>%
  mutate(weights = 1)
br_con <- br %>%
  filter(leg_black == 0) %>%
  mutate(weights = eb$w)
br <- bind_rows(br_treat, br_con)

m <- lm(responded ~ leg_black, data = br, weights = weights)
msummary(m, stars = c('*' = .1, '**' = .05, '***' = .01))

5. Propensity Score Matching

library(causalweight); library(tidyverse)
br <- causaldata::black_politicians

# We can estimate our own propensity score
m <- glm(leg_black ~ medianhhincom + blackpercent + leg_democrat,
         data = br, family = binomial(link = 'logit'))
# Get predicted values
br <- br %>%
    mutate(ps = predict(m, type = 'response'))
# "Trim" control observations outside of
# treated propensity score range
# (we'll discuss this later in Common Support)
minps <- br %>%
    filter(leg_black == 1) %>%
    pull(ps) %>%
    min(na.rm = TRUE)
maxps <- br %>%
    filter(leg_black == 1) %>%
    pull(ps) %>%
    max(na.rm = TRUE)
br <- br %>%
    filter(ps >= minps & ps <= maxps)

# Create IPW weights
br <- br %>%
    mutate(ipw = case_when(
    leg_black == 1 ~ 1/ps,
    leg_black == 0 ~ 1/(1-ps)))

# And use to weight regressions (The standard errors will be wrong
# here unless we bootstrap the whole process - See the code examples
# from the doubly robust estimation section or the simulation chapter)
lm(responded ~ leg_black, data = br, weights = ipw)

# Or we can use the causalweight package!
# First, pull out our variables
# Outcome
Y <- br %>%
    pull(responded)
# Treatment
D <- br %>%
    pull(leg_black)
# Matching variables
X <- br %>%
    select(medianhhincom, blackpercent, leg_democrat) %>%
    as.matrix()

# Note by default this produces average treatment effect,
# not average treatment on the treated, and trims propensity
# scores based on extreme values rather than matching treated range
IPW <- treatweight(Y, D, X, trim = .001, logit = TRUE)

# Estimate and SE
IPW$effect
IPW$se

6. Estimation with Matched Data

# 检验面板平衡
library(Matching)
MatchBalance(Y ~ D + X)

library(boot); library(tidyverse)
br <- causaldata::black_politicians

# Function to do IPW estimation with regression adjustment
ipwra <- function(br, index = 1:nrow(br)) {
  # Apply bootstrap index
  br <- br %>% slice(index)

  # estimate and predict propensity score
  m <- glm(leg_black ~ medianhhincom + blackpercent + leg_democrat,
           data = br, family = binomial(link = 'logit'))
  br <- br %>%
    mutate(ps = predict(m, type = 'response'))

  # Trim control observations outside of treated PS range
  minps <- br %>%
    filter(leg_black == 1) %>%
    pull(ps) %>%
    min(na.rm = TRUE)
  maxps <- br %>%
    filter(leg_black == 1) %>%
    pull(ps) %>%
    max(na.rm = TRUE)
  br <- br %>%
    filter(ps >= minps & ps <= maxps)

  # Create IPW weights
  br <- br %>%
    mutate(ipw = case_when(
      leg_black == 1 ~ 1/ps,
      leg_black == 0 ~ 1/(1-ps)))

  # Estimate difference
  w_means <- br %>%
    group_by(leg_black) %>%
    summarize(m = weighted.mean(responded, w = ipw)) %>%
    arrange(leg_black)

  return(w_means$m[2] - w_means$m[1])
}

b <- boot(br, ipwra, R = 200)
# See estimate and standard error
b

C. Simulation

1. Why We Simulate

测试估计在特定的样本中是否会有真正的效果，进而了解估计的抽样分布

同时，可以看到估计对某些假设的敏感性。验证某一假设不成立时，估计的有效性

library(tidyverse)
set.seed(1000)

# We must pick a number of observations, here 200
d <- tibble(eps = rnorm(200), # by default mean 0, sd 1
    Y = runif(200), # by default from 0 to 1
    X = sample(0:1, # sample from values 0 and 1
               200, # get 200 observations
               replace = TRUE, # sample with replacement
               prob = c(.8, .2))) # Be 1 20% of the time

2. Coding

创建数据

library(tidyverse)
library(purrr)
set.seed(1000)

# N for number of individuals, T for time periods
create_clus_data <- function(N = 200, T = 10) {
    # We're going to create errors clustered at the ID level.
    panel_data <- crossing(ID = 1:N, t = 1:T) %>%
        # Individual/time-varying data
        mutate(W = runif(n(), 0, .1))

    # Now an individual-specific error cluster
    indiv_data <- tibble(ID = 1:N,
                         C = rnorm(N))

    # Join them
    panel_data <- panel_data %>%
        full_join(indiv_data, by = 'ID') %>%
        # Create X, caused by W1 and W2
        mutate(X = 2*W + rnorm(n())) %>%
        # The error term has two components: the individual
        # cluster C, and the individual-and-time-varying element
        mutate(Y = 3*X + (C + rnorm(n())))

    return(panel_data)
}

create_clus_data(100,5)

# A function for estimation
est_model <- function(N, T) {
  # Get our data. This uses create_clus_data from earlier
  d <- create_clus_data(N, T)

  # Run a model that should be unbiased
  # if clustered errors themselves don't bias us!
  m <- lm(Y ~ X + W, data = d)

  # Get the efficient on X, which SHOULD be true value 3 on average
  x_coef <- coef(m)['X']

  return(x_coef)
}

# Run our model
est_model(200, 5)

# Estimate our model 1000 times (from 1 to 1000)
estimates <- 1:1000 %>%
  # Run the est_model function each time
  map_dbl(function(x) est_model(N = 200, T = 5))

3. Power Analysis

library(tidyverse); library(purrr); library(broom)
set.seed(1000)

# Follow the description in the text for data creation. Since we want
# to get minimum sample size and minimum detectable effect, allow both
# sample size and effect to vary.
# diff is the difference in effects between boys and girls
create_data <- function(N, effect, diff) {
    d <- tibble(W = rnorm(N),
        girl = sample(0:1, N, replace = TRUE)) %>%
        # A one-SD change in W makes treatment 10% less likely
        mutate(Training = runif(N) + .1*W < .5) %>%
        mutate(Test = effect*Training + diff*girl*Training +
                      4*W + rnorm(N, sd = 9))

    return(d)
}

# Our estimation function
est_model <- function(N, effect, diff) {
    d <- create_data(N, effect, diff)

    # Our model
    m <- lm(Test~girl*Training + W, data = d)
    tidied <- tidy(m)

    # By looking we can spot that the interaction
    # term is in the 5th row
    sig <- tidied$p.value[5] < .05

    return(sig)
}

# Iteration function!
iterate <- function(N, effect, diff, iters) {
    results <-  1:iters %>%
    map_dbl(function(x) {
        # To keep track of progress
        if (x %% 100 == 0) {print(x)}

        # Run our model and return the result
        return(est_model(N, effect, diff))
    })

    # We want to know statistical power,
    # i.e., the proportion of significant results
    return(mean(results))
}

# Let's find the minimum sample size
mss <- tibble(N = c(10000, 15000, 20000, 25000))
mss$power <- c(10000, 15000, 20000, 25000) %>%
    # Before we had to do function(x) here, but now the argument we're
    # passing is the first argument of iterate() so we don't need it
    map_dbl(iterate, effect = 2, diff = .8, iter = 500)
# Look for the first N with power above 90%
mss

# Now for the minimum detectable effect
mde <- tibble(effect = c(.8, 1.6, 2.4, 3.2))
mde$power <-  c(.8, 1.6, 2.4, 3.2) %>%
    map_dbl(function(x) iterate(N = 2000, effect = 2,
      diff = x, iter = 500))
# Look for the first effect wth power above 90%
mde

4. Bootstrap

library(tidyverse); library(boot)
set.seed(1000)

# Get our data set
data(mtcars)

# Our estimation function. The first argument must be the data
# and the second the indices defining the bootstrap sample
est_model <- function(d, index) {
    # Run our model
    # Use index to pick the bootstrap sample
    m <- lm(hp ~ mpg + wt, data = d[index,])

    # Return the estimate(s) we want to bootstrap
    return(c(coef(m)['mpg'],
             coef(m)['wt']))
}

# Now the bootstrap call!
results <- boot(mtcars,    # data
                est_model, # Estimation function,
                1000)      # Number of bootstrap simulations

# See the coefficient estimates and their bootstrap standard errors
results

Others

# T test
library(tidyverse)
(t.t.df <- data.frame(data$group, data$x1, data$x2) %>%
    select_if(is.numeric) %>%
    map_df(~ broom::tidy(t.test(. ~ data$group))))

1. Structural Equation

# set relevant data into new data frame
SR <- data1[,54:56];
# alpha and omega test
alpha(SR); omega(SR)
# test validity
KMO(SR); cortest.bartlett(SR)

2. Path Analysis

"Path Analysis"
# use likelihood = "wishart" to make result similar to AMOS
# use se = "bootstrap" in sem function if needed
model <- "# define structure
          PBb ~ b1 * SI + b2 * SC + c1 * MH + c2 * FM + c3 * SR +
                c4 * ew + c5 * PltStatus + c6 * Mar + pc + cb +
                Gender + Age + Punishment + Location
          SI ~ a11 * MH + a12 * FM + a13 * SR + Gender + Age
          SC ~ a21 * ew + a22 * PltStatus + a23 * Mar + Gender + Age

          # define indirect pathway
          # MH-SI-PB
          indirect1 := a11 * b1
          # FM-SI-PB
          indirect2 := a12 * b1
          # SR-SI-PB
          indirect3 := a13 * b1
          # ew-SC-PB
          indirect4 := a21 * b2
          # PltStatus-SC-PB
          indirect5 := a22 * b2
          # Mar-SC-PB
          indirect6 := a23 * b2
          # difference between SC and SI
          contrast := indirect1 + indirect2 + indirect3 -
                      indirect4 - indirect5 - indirect6
          total := c1 + c2 + c3 + c4 + (a11*b1) + (a12*b1) + (a13*b1) +
                  (a21*b2) + (a22*b2) + (a23*b2)
"; fit.pa <- sem(model, data = data1, likelihood = "wishart", se = "bootstrap")
summary(fit.pa, fit = T, rsquare = T)
Share this post on:
Share this post via WhatsApp Share this post on Facebook Share this post on X Share this post via Telegram Share this post on Pinterest Share this post via email
Previous Post
R：机器学习
Next Post
浏览器工具合集